A Cold-Weather Experiment
Back to Basics
Back to Basics is a monthly column written by Marshall Chasin for the Hearing Review. Permission has been granted to reprint some of these columns in Canadian Audiologist.

Over the holiday season I fulfilled one of my “bucket list” items—I flew north of 70° latitude in the middle of winter with temperatures hovering around -40°F, and the sun only hints at rising for a minute or two around noon. Well, the -40°F temperature part wasn’t on my bucket list, but the going to the far north to see the Aurora Borealis was. The town of Tromso, Norway, is located more than 200 miles north of the Arctic Circle. Tromso is the third largest town north of the Arctic Circle (whose population is only exceeded by Murmansk and Norilsk in Siberia).
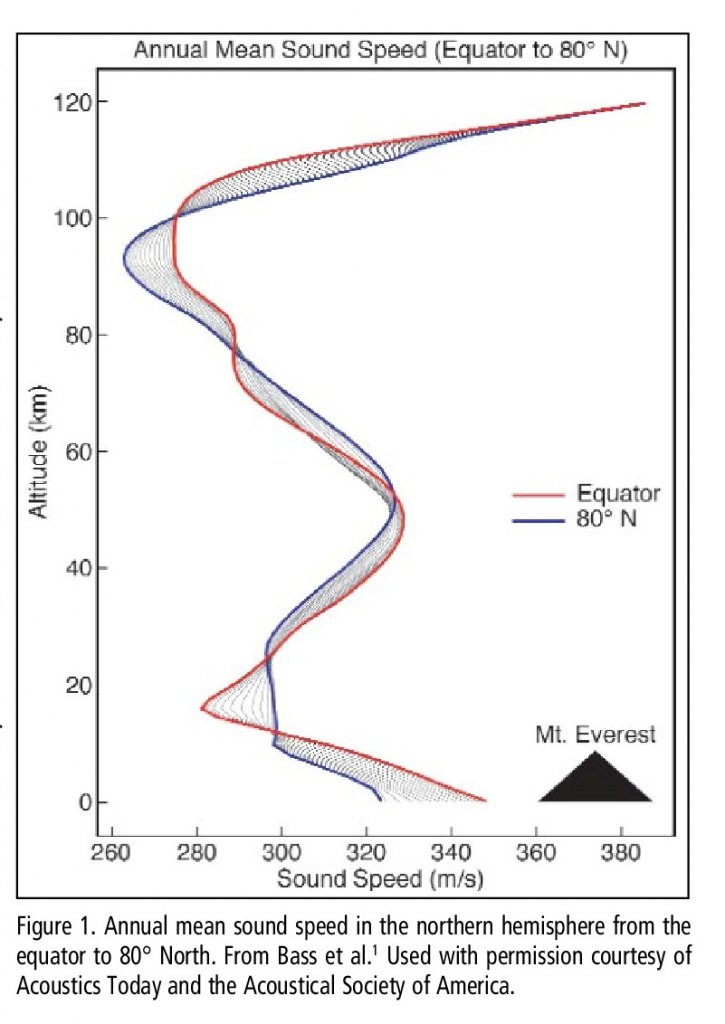
One of the first things that I did after arriving is to calculate the speed of sound. Well, I didn’t need to calculate it; I just used a handy figure that I always carry with me that provides the speed of sound at the Equator and at 80°N latitude relative to altitude (Figure 1). At home, the speed of sound is roughly 340 meters/sec, or 1/3 of a kilometer/sec. If lightning strikes, and if thunder is heard 3 seconds later, then I know that the strike was about a kilometer (0.6 miles) away. But in the far north, the speed of sound is closer to 320 meters/sec. Actually, it’s even lower since the speed of sound is a function of environmental temperature (V = 20.05 x (absolute T)0.5). and the speed was prob-ably closer to 300 meters/sec. In any event, the speed of sound in the Arctic is much lower than at home. Given that frequency = speed of sound/wave-length, for any given wavelength, the frequency (in Hz) would be lower. Yet, when I listened to music or tried to talk to people (which was almost impossible given that industrial grade earmuffs for the cold provide 1000 dB of attenuation), I had no difficulty understanding them or appreciating my music. The music certainly did not sound flat to my ear, even though the frequency was indeed flat. I am positive that one of my colleagues who has perfect pitch may have noticed a problem, but I certainly didn’t. This would make for an interesting AuD Capstone project for an interested student who does have perfect pitch (and likes cold weather and no sun and $24 beers).
The issue is that in perception we rarely need to hear the exact frequency (or frequency spectrum) of speech or of music. However, we do need to hear the relative differences in spectral cues. For the vowel [a] as in “father,” there are formants at 500 Hz, 1500 Hz, and 2500 Hz—the odd numbered multiples of 500 Hz. But we need to hear the relative differences between the formants and not just the absolute frequencies of the formants. Hearing a “difference” of 1000 Hz, or at least the same difference between the various formants (whatever that may be), allows us to hear the vowel [a] in “father.” This is similar to listening to Baroque music. Because of the age of many of the musical instruments, they tend to be tuned at a slightly lower frequency than modern instruments. The note A (440 Hz) may be tuned to A (425 Hz). Baroque music sounds great to me and certainly does not sound flat. However, the medical director at the Musicians’ Clinics of Canada who has perfect pitch, cringes at that sound. Thank goodness that I am a mere mortal! In Germany, some orchestras tune slightly sharp to A (445Hz) but again, the music still sounds great, at least to my ear. It’s not the absolute values, but the relative differences that define good music (and speech) quality.

